SKKN Các phương pháp chứng minh tứ giác nội tiếp và bài tập vận dụng tứ giác nội tiếp

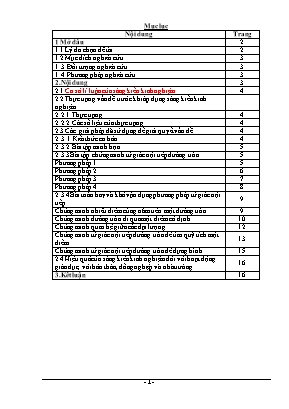
Mục lục
Nội dung
Trang
1 Mở đầu
2
1.1 Lý do chọn đề tài 
2
1.2 Mục đích nghiên cứu
3
1.3. Đối tượng nghiên cứu
3
1.4. Phương pháp nghiên cứu
3
2.Nội dung 
3
2.1 Cơ sở lí luận của sáng kiến kinh nghiệm
4
2.2 Thực trạng vấn đề trước khi áp dụng sáng kiến kinh nghiệm.
2.2.1. Thực trạng
4
2.2.2. Các số liệu của thực trạng
4
2.3 Các giải pháp đã sử dụng để giải quyết vấn đề
4
2.3.1.Kiến thức cơ bản
4
2.3.2. Bài tập minh họa
5
2.3.3 Bài tập chứng minh tứ giác nội tiếp đường tròn
5
Phương pháp 1
5
Phương pháp 2
6
Phương pháp 3
7
Phương pháp 4
8
2.3.4 Bài toán hay và khó vận dụng phương pháp tứ giác nội tiếp
9
Chứng minh nhiều điểm cùng nằm trên một đường tròn.
9
Chứng minh đường tròn đi qua một điểm cố định.
10
Chứng minh quan hệ giữa các đại lượng.
12
Chứng minh tứ giác nội tiếp đường tròn để tìm quỹ tích một điểm.
13
Chứng minh tứ giác nội tiếp đường tròn để dựng hình.
15
2.4 Hiệu quả của sáng kiến kinh nghiệm đối với hoạt động giáo dục, với bản thân, đồng nghiệp và nhà trường
16
3.Kết luận
16
Phần I – Mở đầu
I – Lí do chọn đề tài 
Như chúng ta đều biết toán học là một bộ môn khoa học tự nhiên mang tính trừu tượng cao, tính logíc đồng thời môn toán còn là bộ môn công cụ hỗ trợ cho các môn học khác.Với môn hình học là môn khoa học rèn luyện cho học sinh khả năng đo đạc, tính toán, suy luận logíc, phát triển tư duy sáng tạo cho học sinh
Trong hoạt động giáo dục hiện nay, đòi hỏi học sinh cần phải tự học tự nghiên cứu rất cao. Tức là cái đích cần phải biến quá trình giáo dục thành quá trình tự giáo dục. Như vậy, học sinh có thể phát huy được năng lực sáng tạo, tư duy khoa học, từ đó xử lý linh hoạt được các vấn đề của đời sống xã hội. 
Một trong những phương pháp để giúp học sinh đạt được điều đó đối với môn Toán (cụ thể môn Hình Học 9) đó là khích lệ các em sau mỗi đơn vị kiến thức cần khắc sâu, tìm tòi những bài toán liên quan. Làm được như vậy có nghĩa là các em rất cần sự say mê học tập, tự nghiên cứu đào sâu kiến thức.
Đối với học sinh lớp 9 khi học các bài toán về đường tròn thì chuyên đề tứ giác nội tiếp và những bài toán liên quan đến tứ giác nội tiếp là rất quan trọng. Đóng vai trò là đơn vị kiến thức trọng tâm của nội dung Hình Học lớp 9. Mà đa số các em mới chỉ biết đến chứng minh một tứ giác nội tiếp đường tròn là như thế nào, còn ít biết vận dụng phương pháp tứ giác nội tiếp để làm gì ? 
Ta biết rằng có nhiều phương pháp để chứng minh một tứ giác là nội tiếp đường tròn. Khi biết một tứ giác nội tiếp đường tròn thì suy ra được góc trong ở một đỉnh bằng góc ngoài ở đỉnh đối diện với nó hay vận dụng các Định lý về mối liên hệ giữa các loại góc của đường tròn để tìm ra những cặp góc bằng nhau. Với phương pháp tứ giác nội tiếp ta có thể vận dụng để giải một số bài toán hay và khó .
Với lý do đó, tôi đã chọn đề tài nghiên cứu cho mình là: “Các phương pháp chứng minh tứ giác nội tiếp và bài tập vận dụng tứ giác nội tiếp”
II – Mục đích và đối tượng nghiên cứu:
Nghiên cứu đề tài nhằm mục đích giúp giáo viên nắm rõ các phương pháp chứng minh tứ giác nội tiếp đồng thời vận dụng phương pháp tứ giác nội tiếp để giải một số bài toán hay và khó như sau: 
Chứng minh nhiều điểm cùng nằm trên một đường tròn.
Chứng minh đường tròn đi qua một điểm cố định.
Chứng minh quan hệ giữa các đại lượng.
Chứng minh tứ giác nội tiếp đường tròn để tìm quỹ tích một điểm.
Chứng minh tứ giác nội tiếp đường tròn để dựng hình.
Như vậy, giáo viên có thể giúp học sinh nắm vững, khai thác sâu, đầy đủ một cách có hệ thống đơn vị kiến thức “Tứ giác nội tiếp trong một đường tròn”.
III – Phương pháp nghiên cứu
Để nghiên cứu đề tài này, tôi đã sử dụng các phương pháp cơ bản sau: 
1. Phương pháp nghiên cứu lý thuyết 
Kết hợp kinh nghiệm giảng dạy,tham khảo ý kiến của đồng nghiệp có được với sự nghiên cứu tài liệu, tôi đã sử dụng các tài liệu như: 
- Sách giáo khoa Toán 9 (tập II – NXB Giáo dục)
- Sách bài tập Toán 9 (tập II – NXB Giáo dục)
- Toán nâng cao Hình học 9 – NXB Thành phố Hồ Chí Minh
- Toán nâng cao và các chuyên đề 9 – NXB Giáo dục.
- Các bài toán hay và khó về đường tròn – NXB Đà Nẵng.
- Nâng cao và phát triển toán 9 tập II – NXB Giáo dục
- Các đề thi tuyển sinh vào lớp 10 chuyên – NXB Đại học sư phạm
2. Phương pháp nghiên cứu thực tiễn.
Tôi tiến hành dạy thử nghiệm đối với học sinh lớp 9D4; D2 – Trường THCS Nguyễn Du – Quảng Xương và bồi dưỡng đội tuyển học sinh Giỏi của trường.
3. Phương pháp đánh giá.
Kết thúc chuyên đề đối với học sinh lớp 9D4; D2, tôi có tiến hành kiểm tra đánh giá mức độ nhận thức và suy luận của các em.
PHẦN II: NỘI DUNG 
I. Thực trạng của vấn đề nghiên cứu:
1. Thực trạng :
a) Thuận lợi:
Được sự chỉ đạo của Ban giám hiệu nhà trường trong các hoạt động đặc biệt trong họat động chuyên môn, luôn tạo mọi điều kiện cho giáo viên phấn đấu, học tập và nghiên cứu, phát huy các phương pháp dạy học đổi mới sáng tạo nhất. Bên cạnh đó trường THCS Nguyễn Du đã và đang xây dựng thành trường trọng điểm chất lượng cao của huyện Quảng Xương điều này thúc đẩy các giáo viên nói chung và giáo viên dạy toán nói riêng và học sinh phải năng động tìm tòi, tư duy sáng tạo trong việc dạy và học toán. Mặt khác, nhà trường có nhiều học sinh khá giỏi nên đối tượng mà tôi áp dụng đến cũng gặp nhiều thuận lợi hơn. 
b) Khó khăn: 
Bên cạnh những mặt thuận lợi cũng có nhiều những khó khăn như: tài liệu tham khảo thêm cũng còn đang hạn chế, bản tân mặc dù cũng đã dạy HSG nhiều năm nhưng kinh nghiệm vẫn cần được tích lũy thêm, số học sinh độc lập tư duy sáng tạo không nhiều.
Chính vì vậy càng cần phải rèn luyện cho các em năng lực tư duy độc lập sáng tạo,có phương pháp suy luận rõ ràng càng khiến tôi tâm huyết tìm tòi, nghiên cứu đề tài này.
2. Các số liệu của thực trạng : 
Qua các năm giảng dạy trực tiếp bồi dưỡng cho học sinh nói chung và học sinh khá giỏi nói riêng, qua trắc nghiệm hứng thú học toán của học sinh tôi thấy chỉ có 25% các em thực sự có hứng thú học toán (có tư duy sáng tạo), 45% học sinh thích học toán (chưa có tính độc lập, tư duy sáng tạo) và 30% còn lại nửa thích nửa không . Qua gần gủi tìm hiểu thì các em cho biết cũng rất muốn học xong nhiều khi học một cách thụ động, chưa biết cách tư duy để tạo cho mình một phương pháp giải phù hợp với từng loại toán trong một bài toán nào đó, bởi vì do tâm lí người học chỉ học để phục vụ cho thi chứ chưa phải vì sự say mê do vậy học sinh chưa có hứng thú học toán và kết quả qua các kì thi chưa cao.
II – Nội dung cụ thể
1 – Kiến thức cơ bản 
1.1 Khái niệm tứ giác nội tiếp 
* Tứ giác nội tiếp đường tròn là tứ giác có bốn đỉnh nằm trên đường tròn đó.
* Trong hình 1, tứ giác ABCD nội tiếp (O) và (O) ngoại tiếp tứ giác ABCD.
Hình 1
1.2.Định lý.
	* Trong một tứ giác nội tiếp tổng số đo hai góc đối diện bằng180o.
* Nếu một tứ giác có tổng số đo hai góc đối diện bằng180o thì tứ giác đó nội tiếp được một đường tròn.
Tứ giác ABCD nội tiếp đường tròn Û ÐA + ÐC = 1800 hoặc ÐB + ÐD = 1800
1.3. Một số phương pháp chứng minh tứ giác nội tiếp 
Tứ giác có tổng hai góc đối bằng 1800.
Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.
Tứ giác có 4 đỉnh cách đều một điểm (mà ta có thể xác định được). Điểm đó là tâm của đường tròn ngoại tiếp tứ giác.
Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc a .
1.4. Một số bài toán hay và khó vận dụng phương pháp tứ giác nội tiếp.
Chứng minh nhiều điểm cùng nằm trên một đường tròn.
Chứng minh đường tròn đi qua một điểm cố định.
Chứng minh quan hệ giữa các đại lượng.
Chứng minh tứ giác nội tiếp đường tròn để tìm quỹ tích một điểm.
Chứng minh tứ giác nội tiếp đường tròn để dựng hình.
2 - Bài tập minh hoạ
2.1. Bài tập chứng minh tứ giác nội tiếp đường tròn.
Phương pháp 1: Dựa vào định nghĩa.
Bài toán 1: 
 Cho tam giác ABC, 2 đường cao BB’, CC’. Chứng minh tứ giác BCB’C’ nội tiếp.
Chứng minh: 
Cách 1: 	Lấy O là trung điểm của cạnh BC.
Xét DBB’C có : Ð BB’C = 900 (GT)
	OB’ là đường trung tuyến ứng với cạnh huyền 
	Þ OB’ = OB = OC = r (1)
Xét DBC’C có : Ð BC’C = 900 (GT)
	Tương tự trên Þ OC’ = OB = OC = r (2)
Từ (1) và (2) Þ B, C’, B’, C Î (O; r) 
	Þ Tứ giác BC’B’C nội tiếp đường tròn.
Cách 2: Ta có: 	BB’ ^ AC (GT) Þ Ð BB’C = 900.
	CC’ ^ AB (GT) Þ Ð BC’C = 900.
	Þ B’, C’ cùng nhìn cạnh BC dưới một góc vuông 
	Þ B’, C’ nằm trên đường tròn đường kính BC
	Hay Tứ giác BC’B’C nội tiếp đường tròn đường kính BC.
Phương pháp 2: Dựa vào định lý
Tứ giác ABCD nội tiếp đường tròn Û ÐA + ÐC = 1800 
 hoặc ÐB + ÐD = 1800
Bài toán 2: 
 Cho tam giác ABC nhọn và nội tiếp (O), 2 đường cao BB’, CC’. 
a/ Chứng minh tứ giác BCB’C’ nội tiếp.
b/ Tia AO cắt (O) ở D và cắt B’C’ ở I. Chứng minh tứ giác BDIC’ nội tiếp.
Chứng minh: 
a/ (Bài toán 1) 
b/ Từ câu a 	Þ Ð C + Ð BC’B’ = 1800
	(Tổng hai góc đối của tứ giác nội tiếp)
Mà : Ð C = Ð D (hai góc nội tiếp cùng chắn cung AB)
Þ Ð D + Ð BC’I = 1800
Þ Tứ giác BDIC’ nội tiếp đường tròn.
Phương pháp 3: Dựa vào quỹ tích cung chứa góc 
Bài toán 3: 
Cho D ABC cân ở A nội tiếp (O). Trên tia đối của tia AB lấy điểm M, trên tia đối của tia CA lấy điểm N sao cho AM=CN. 
 Chứng minh Tứ giác AMNO nội tiếp.
Chứng minh:
	Ta có: D ABC cân ở A và O là tâm đường tròn ngoại tiếp D ABC 
Þ Ð A1 = Ð A2
DAOC cân tại O (vì OA = OC)
Þ ÐA2 = ÐC1 nên ÐA1 = ÐA2 = ÐC1 
Mà ÐA1 + ÐOAM = 1800 và ÐC1+ ÐOCN= 1800.
Þ ÐAOM = ÐOCN
Xét DOAM và DOCN có : OA = OC; ÐAOM = ÐOCN; AM = CN
DOAM = DOCN (c.g.c)
ÐAMO = ÐCNO hay ÐAMO = ÐANO
Tứ giác AMNO nội tiếp đường tròn (hai đỉnh kề nhau M và N cùng nhìn cạnh OA dưới cùng một góc).
Phương pháp 4: Dựa vào: tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.
Bài toán 4:
Cho tứ giác ABCD nội tiếp (O), M là điểm chính giữa của cung AB. Nối M với D, M với C cắt AB lần lượt ở E và P. 
Chứng minh tứ giác PEDC nội tiếp được đường tròn.
Chứng minh: 
Ta có : Ð MEP là góc có đỉnh nằm bên trong (O)
Mà 	 (góc nội tiếp)
Hay 	
Lại có : 	
Nên : 	= 
Nghĩa là: Tứ giác PEDC có góc ngoài tại đỉnh E bằng góc trong tại đỉnh C
Vậy Tứ giác PEDC nội tiếp được đường tròn.
Bài toán 5: (Bài tập tổng hợp các phương pháp chứng minh tứ giác nội tiếp)
Cho hình vẽ: 
 Biết AC ^ BD tại O, OE ^AB tại E; OF ^ BC tại F; OG ^ DC tại G; OH ^AD tại H.
 Hãy tìm các tứ giác nội tiếp trong hình vẽ bên.
Chứng minh:
* Các tứ giác nội tiếp vì có hai góc đối là góc vuông là:
AEOH; BFOE; CGOF; DHOG
* Các tứ giác nội tiếp vì có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện 
AEFC; AHGC; BEHD; BFGD
Thật vậy: 	Xét tứ giác AEFC 
	Ta có: ÐEAC = Ð EOB (cùng phụ với Ð ABO)
	Ð BFE = ÐEOB (Hai góc nội tiếp cùng chắn cung EB)
	Þ ÐEAC = Ð BFE.
Các tứ giác AHGC; BEHD; BFGD chứng minh tương tự.
* Tứ giác EFGH nội tiếp vì có tổng hai góc đối bằng 1800
Thật vậy: Ta có : 	Ð OEH = ÐOAH ( vì cùng chắn cung OH)
	ÐOAH = ÐHOD (vì cùng phụ với ÐAOH)
	ÐHOD = ÐHGD ( vì cùng chắn cung HD)
Þ Ð OEH =ÐHGD 
Chứng minh tương tự ta được : ÐOEF = ÐFGC
Từ đó : Ð OEH + ÐOEF =ÐHGD + ÐFGC
Þ Ð FEH =ÐHGD + ÐFGC
Mặt khác: ÐHGD + ÐFGC+ ÐHGF = 1800
Þ Ð FEH + ÐHGF = 1800 ( điều phải chứng minh)
2.2. Bài toán hay và khó vận dụng phương pháp tứ giác nội tiếp
Bài toán 1. Chứng minh nhiều điểm cùng nằm trên một đường tròn.
a. Phương pháp: 
Nếu ta phải chứng minh 5 điểm A, B, C, D, E cùng nằm trên một đường tròn, ta có thể chứng minh tứ giác ABCD nội tiếp và tứ giác ABCE nội tiếp. Suy ra 4 điểm A, B, C, D và 4 điểm A, B, C, E cùng nằm trên một đường tròn. Hai đường tròn này có ba điểm chung là A, B, C thế nên theo định lý về sự xác định đường tròn thì chúng phải trùng nhau. Từ đó suy ra 5 điểm A, B, C, D, E cùng nằm trên một đường tròn.
b. Ví dụ 1: (Bài toán về đường tròn Euler)
Chứng minh rằng, trong một tam giác bất kì, ba trung điểm của các cạnh, ba chân của các đường cao, ba trung điểm của các đoạn thẳng nối trực tâm với đỉnh đều ở trên một đường tròn.
Chứng minh:
Ta có: ME là đường trung bình của DAHC 
ND là đường trung bình của DBHC
Þ ME = ND = HC/2
Þ tứ giác MNDE là hình bình hành (1)
Lại có : ME // CH; MN // AB (vì MN là đường trung bình của DHAB)
Mà CH ^ AB (GT)
Þ ME ^ MN (2)
Từ (1) và (2) Þ Tứ giác MNDE là hình chữ nhật
Gọi O là trung điểm của MD Þ O cũng là trung điểm của NE
Nên hình chữ nhật MNDE nội tiếp (O; OM)
Chứng minh tương tự ta được hình chữ nhật FMPD cũng nội tiếp (O; OM)
Vì Ð MID = 900 Þ I Î (O; OM)
Vì Ð FLP = 900 ; Ð NKE = 900 Þ L; K Î (O; OM)
Vậy ta có : 9 điểm M; K; E; P; D; I; N; F; L Î (O; OM)
	 	(Điều phải chứng minh)
c.Bài tập:
1. Cho hình bình hành ABCD có Ð A nhọn. Đường tròn tâm A bán kính AB cắt đường thẳng BC ở điểm thứ hai E. Đường tròn tâm C bán kính CB cắt đường thẳng AB ở điểm thứ hai K. Chứng minh rằng:
a. DE = DK
b. năm điểm A, D, C, K, E cùng thuộc một đường tròn.
2. Cho hai đường tròn (O) và (O’) ở ngoài nhau.Kẻ các tiếp tuyến chung ngoài AB và A’B’, các tiếp tuyến chung trong CD và EF (A, A’, C, E Î (O); B, B’, D, F Î (O’)). Gọi M là giao điểm của AB và EF, N là giao điểm của CD và A’B’. H là giao điểm của MN là OO’. Chứng minh rằng:
a. MN ^ OO’
b. năm điểm O’, B, M, H, F cùng thuộc một đường tròn
c. năm điểm O, A, M, E, H cùng thuộc một đường tròn
Bài toán 2. Chứng minh đường tròn đi qua một điểm cố định.
a. Phương pháp:
Nếu ta phải chứng minh một đường tròn (ABC) đi qua một điểm cố định, 
Cách 1: Ta có thể xét thêm một điểm D cố định nào đó rồi chứng minh tứ giác ABCD nội tiếp đường tròn. Từ đó suy ra điều phải chứng minh.
Cách 2: Ta chọn một điểm nào đó trên đường tròn (ABC) sau đó ta đi chứng minh điểm đã chọn là điểm cố định.
b. Ví dụ 1: 
Cho đường tròn tâm O đường kính AB, điểm C cố định trên đường kính ấy (C khác O). Điểm M chuyển động trên đường tròn. Đường vuông góc với AB tại C cắt MA, MB theo thứ tự ở E và F. Chứng minh rằng đường tròn ngoại tiếp tam giác AEF luôn đi qua một điểm cố định khác A.
Chứng minh:
Gọi K là giao điểm của đường tròn đi qua ba điểm A, E, F với AB. 
Nối K với F
Ta có 	Ð F1 = Ð A ( cùng bằng nửa số đo cung KE)
 	Ð F2 = Ð A ( cùng phụ với Ð MBA)
Þ Ð F1 = Ð F2 
Þ K đối xứng với B qua C
Do B và C là hai điểm cố định nên suy ra K cố định
Vậy đường tròn ngoại tiếp tam giác AEF đi qua điểm K cố định.
Ví dụ 2: 
Từ một điểm A ở ngoài đường tròn (O) ta vẽ hai tiếp tuyến AB, AC với đường tròn. Lấy điểm D nằm giữa B và C. Qua D vẽ một đường thẳng vuông góc với OD cắt AB, AC lần lượt tại E và F.
 Khi điểm D di động trên BC, chứng minh rằng đường tròn (AEF) luôn đi qua một điểm cố định khác A.
Chứng minh:
Ta có : 	Ð EBO = 900 (AB là tiếp tuyến với (O) tại B)
	Ð EDO = 900 (GT)
Þ hai đỉnh B và D cùng nhìn đoạn OE dưới một góc vuông.
Þ Tứ giác EBOD nội tiếp đường tròn
Þ Ð BEO = Ð BDO (1) (cùng chắn cung OB)
Chứng minh tương tự ta có : Tứ giác ODCF nội tiếp đường tròn 
Þ Ð OFC = Ð BDO (2) (góc trong một đỉnh bằng góc ngoài tại đỉnh đối diện)
Từ (1) và (2) Þ Ð OFC = Ð BEO 
Þ Tứ giác AEOF nội tiếp đường tròn (theo dấu hiệu góc trong một đỉnh bằng góc ngoài tại đỉnh đối diện)
Vậy đường tròn (AEF) đi qua điểm O cố định.
c. Bài tập: 
1. Cho tam giác ABC nội tiếp (O), I là điểm chính giữa của cung BC không chứa A. Vẽ (O1) đi qua I và tiếp xúc với AB tại B, vẽ (O2) đi qua I và tiếp xúc với AC tại C. Gọi K là giao điểm thứ hai của hai đường tròn (O1) và (O2).
a/ Chứng minh rằng ba điểm B, K, C thẳng hàng.
b/ Lấy điểm D bất kì thuộc cạnh AB, điểm E thuộc tia đối của tia CA sao cho BD = CE. Chứng minh rằng đường tròn ngoại tiếp tam giác ADE luôn đi qua một điểm cố định khác A.
Bài toán 3. Chứng minh quan hệ về đại lượng.
Một số bài toán đề cập tới quan hệ về đại lượng như: 
- Chứng minh các hệ thức hình học( đoạn thẳng bằng nhau; góc bằng nhau; hệ thức ....)
- Chứng tỉ số các đoạn thẳng không đổi (như hai đoạn thẳng bằng nhau, đoạn này gấp đôi đoạn kia.) hoặc chứng minh tổng hiệu các góc là không đổi....
* Định lý Ptô - lê mê.
Chứng minh rằng trong một tứ giác nội tiếp, tích của hai đường chéo bằng tổng các tích của hai cặp cạnh đối.
Chứng minh:
Ta có : Tứ giác ABCD nội tiếp (O)
Ta phải chứng minh: AC. BD = AB. DC + AD. BC
Thật vậy.
Lấy E Î BD sao cho Ð BAC = Ð EAD
Þ D DAE D CAB (g. g)
Þ 
Þ AD. BC = AC. DE (1)
Tương tự: D BAE D CAD (g. g) 
Þ 
Þ BE. AC = CD. AB (2)
Từ (1) và (2) Þ AD. BC + AB. CD = AC. DE + EB. AC 
	Þ AD. BC + AB. CD = AC. DB (ĐPCM)
c. Bài tập 
1.Sử dụng Định lý Ptô - lê - mê để chứng minh ( Định lý Các - nô)
Chứng minh rằng tổng các khoảng cách từ tâm của đường tròn ngoại tiếp một tam giác nhọn đến các cạnh của tam giác bằng tổng các bán kính của đường tròn ngoại tiếp và đường tròn nội tiếp tam giác đó. 
2. Cho D ABC nhọn với trực tâm H. Vẽ hình bình hành BHCD. Đường thẳng qua D và song song với BC cắt đường thẳng AH tại E.
a.Chứng minh các điểm A, B, C, D, E cùng thuộc một đường tròn.
b.Gọi O là tâm đường tròn ngoại tiếp D ABC , chứng minh: 
	Ð BAE = Ð OAC và BE = CD.
c. Gọi M là trung điểm của BC, đường thẳng AM cắt OH tại G. Chứng minh G là trọng tâm của D ABC.
Bài toán 4. Chứng minh tứ giác nội tiếp đường tròn để tìm quỹ tích một điểm.
a. Các bước giải bài toán quỹ tích:
Bước1: Chứng minh phần thuận 
 Chứng minh rằng những điểm M có các tính chất đã cho thuộc hình H
+ Giới hạn quỹ tích 
Bước 2: chứng minh phần đảo
Chứng minh mỗi điểm của hình H đề có tính chất đã cho.
Bước 3: Kết luận 
b. Ví dụ 1 :
Cho hình vuông ABCD, tâm O. Một đường thẳng xy quay quanh O cắt hai cạnh AD và BC lần lượt tại M và N. Trên CD lấy điểm K sao cho DK = DM. Gọi H là hình chiếu của K trên xy. Tìm quỹ tích điểm H.
Chứng minh:
Phần thuận:
Ta có CN = AM (tính chất đối xứng tâm)
Vì DK = DM (GT) nên CK = AM 
Þ CK = CN 
Lại có Tứ giác MHKD và Tứ giác NHKC nội tiếp (vì có hai góc đối vuông)
Þ Ð M1 = Ð H1 = 450 và Ð N2 = Ð H2 = 450 
Þ Ð DHC = 900
Vậy H nằm trên đường tròn đường kính DC
Giới hạn:
Vì đường thẳng xy quay quanh O nhưng phải cắt hai cạnh AD và BC lần lượt tại M và N nên điểm H chỉ nằm trên một nửa đường tròn đường kính CD nằm trong hình vuông.
Phần đảo:
Lấy điểm H bất kì trên nửa đường tròn đường kính CD.
Vẽ đường thẳng HO cắt AD và BC lần lượt tại M và N.
Lấy điểm K trên CD sao cho DK = DM.
Ta phải chứng minh H là hình chiếu của K trên MN.
Thật vậy,
Vì Ð DHC =900 ; Ð DOC = 900 nên à HOCD nội tiếp 
Þ Ð DHM = Ð DCO = 450
Mặt khác Ð DKM = 450 nên Ð DHM = Ð DKM 
Þ Tứ giác HKDM nội tiếp Þ Ð KHM = 900 
Þ KH ^ NM 
Þ H là hình chiếu của K trên MN.
Kết luận:
Vậy quỹ tích của điểm H là nửa đường tròn đường kính CD, nửa đường tròn này nằm trong hình vuông.
Bài toán 5 . Chứng minh tứ giác nội tiếp đường tròn để dựng hình.
a. Ví dụ:
Cho tam giác ABC nhọn (AB < AC), điểm D di động trên cạnh BC. Vẽ DE ^ AB, DF ^ AC. Xác định vị trí của điểm D để:
a/ EF có độ dài nhỏ nhất.
b/ EF có độ dài lớn nhất.
Chứng minh:
Gọi O là trung điểm của AD
Tứ giác AEDF có : Ð AED + Ð AFD = 900 + 900 = 1800
Þ Tứ giác AEDF nội tiếp (O; OA)
Vẽ OM ^ EF Þ ME = MF 
Đặt Ð BAC = a
Ta có : Ð EOM = Ð EOF: 2 = Ð BAC = a
Xét D MOE có Ð OME = 900.
Þ EM = OE. sin a 
Þ EF = 2 OE. sin a
Þ EF = AD. sin a (*) ( vì AD = 2OE)
a/ Do a không đổi nên từ (*) suy ra EF nhỏ nhất Û AD nhỏ nhất Û AD ^ BC Û D là hình chiếu của A trên BC.
b/ Vì D Î BC và AB < AC nên AD £ AC 
Từ (*) Þ EF lớn nhất 	Û AD lớn nhất 
D trùng với C. 
b. Bài tập: 
Cho D ABC nhọn nội tiếp (O). Gọi M là một điểm trên cung ABC. Vẽ MD ^ BC; ME ^ AC; MF ^ AB. Xác định vị trí của M để EF có độ dài lớn nhấ
III – Kết quả thu được
Sau chuyên đề “Các phương pháp chứng minh tứ giác nội tiếp và bài tập vận dụng tứ giác nội tiếp” tôi đã tiến hành dạy thử nghiệm hai lớp với hai đối tượng học sinh: Lớp 9D4 gồm Các em đội tuyển Toán – Lí – Hóa và lớp 9D3 gồm các em có lực học trung bình và khá đã thu được kết quả như sau:
Đối với lớp 9D4: 80% từ điểm 8 trở lên; 10% từ điểm 7 - 8; 10% điểm 6 – 7, không có điểm dưới 6 
Đối với học sinh lớp 9D3: 20% từ điểm 8 trở lên; 50% từ 6 – 8; 30% từ 5 – 6. Không có điểm dưới 5
 Phần III . KẾT LUẬN
Bài học kinh nghiệm
 Đối với giáo viên:
- Cần xác định đúng yêu cầu nhiệm vụ, trách nhiệm và vấn đề bồi dưỡng học sinh giỏi, và vấn đề chất lư