SKKN Kinh nghiệm hướng dẫn học sinh lớp 9 khai thác kiến thức phần Tứ giác nội tiếp - Hình học 9 đạt hiệu quả cao

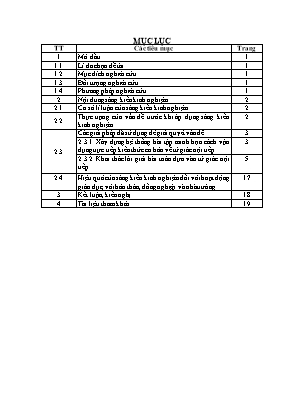
MỤC LỤC
TT
Các tiêu mục
Trang
1
Mở đầu
1
1.1
Lí do chọn đề tài
1
1.2
Mục đích nghiên cứu
1
1.3
Đối tượng nghiên cứu
1
1.4
Phương pháp nghiên cứu
1
2
Nội dung sáng kiến kinh nghiệm	
2
2.1
Cơ sở lí luận của sáng kiến kinh nghiệm
2
2.2
Thực trạng của vấn đề trước khi áp dụng sáng kiến kinh nghiệm
2
2.3
Các giải pháp đã sử dụng để giải quyết vấn đề
3
2.3.1. Xây dựng hệ thống bài tập minh họa cách vận dụng trực tiếp kiến thức cơ bản về tứ giác nội tiếp.
3
2.3.2. Khai thác lời giải bài toán dựa vào tứ giác nội tiếp.
5
2.4
Hiệu quả của sáng kiến kinh nghiệm đối với hoạt động giáo dục, với bản thân, đồng nghiệp và nhà trường
17
3
Kết luận, kiến nghị 
18
4
Tài liệu tham khảo
19
1. MỞ ĐẦU
1.1. Lí do chọn đề tài.
- Toán học là một bộ môn khoa học tự nhiên mang tính logic, tính trừu tượng cao. Đặc biệt là với phân môn Hình học, nó giúp cho học sinh khả năng tính toán, suy luận logic và phát triển tư duy sáng tạo. Việc bồi dưỡng học sinh học toán không đơn thuần chỉ cung cấp cho các em một số kiến thức cơ bản thông qua việc làm bài tập hoặc làm càng nhiều bài tập khó mà giáo viên phải biết rèn luyện khả năng và thói quen suy nghĩ, tìm tòi, khai thác lời giải của một bài toán trên cơ sở những kiến thức đã được trang bị.
- Thực tế cho thấy tâm lí chung của đa số học sinh là sợ và ngại học môn Hình học. Nguyên nhân là do các em chưa tìm được phương pháp học tập phù hợp với đặc trưng bộ môn, vì môn Hình học là môn học khó với lượng bài tập đa dạng, trong đó có nhiều bài tập khó đòi hỏi học sinh không những nắm vững kiến thức cơ bản mà còn phải biết vận dụng linh hoạt, có kĩ năng trình bày suy luận một cách khoa học, logic.
- Tứ giác nội tiếp rất quan trọng trong chương trình Hình học 9 bởi nó gắn liền với mảng kiến thức về đường tròn với nhiều mức độ từ dễ đến khó mà người giáo viên khi giảng dạy có thể khai thác được. Đây cũng là nội dung thường gặp trong các đề thi vào lớp 10 PTTH. Xuất phát từ lí do đó, tôi đã chọn cho mình đề tài nghiên cứu: ‘‘Kinh nghiệm hướng dẫn học sinh lớp 9 khai thác kiến thức phần Tứ giác nội tiếp - Hình học 9 đạt hiệu quả cao” với mong muốn giúp cho các em học sinh có thể tự hình thành cho mình phương pháp học tập hiệu quả, từ đó nắm vững kiến thức và tự tin xử lí các tình huống toán học trong thực tiễn.
1.2. Mục đích nghiên cứu.
- Việc nghiên cứu, lựa chọn đề tài là để nhằm mục đích hướng dẫn HS hệ thống hóa kiến thức, cách thức tiếp cận, khai thác có hiệu quả phần Tứ giác nội tiếp - Hình học 9, khơi gợi sự hứng thú, niềm đam mê môn học nơi học sinh, đồng thời chuẩn bị hành trang kiến thức cho các em chuẩn bị bước vào kì thi vào lớp 10 PTTH.
1.3 Đối tượng nghiên cứu.
	- Đề tài nhằm hướng tới việc nghiên cứu, tổng kết một số đơn vị kiến thức xoay quanh phần Tứ giác nội tiếp - Hình học 9.
1.4. Phương pháp nghiên cứu.
- Phương pháp nghiên cứu lý thuyết kết hợp kinh nghiệm giảng dạy của bản thân.
- Phương pháp nghiên cứu thực tiễn.
	- Phương pháp phát hiện và giải quyết vấn đề.
2. NỘI DUNG CỦA SÁNG KIẾN KINH NGHIỆM
2.1. Cơ sở lí luận của sáng kiến kinh nghiệm. [1]
a) Định nghĩa tứ giác nội tiếp.
	Một tứ giác có 4 đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn (gọi tắt là tứ giác nội tiếp).
B
D
C
A
. O
VD: Trong hình bên, ta có tứ giác ABCD nội tiếp 
đường tròn (O) hay đường tròn (O) ngoại tiếp tứ giác 
ABCD.
b) Định lí:
* Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 1800.
* Nếu một tứ giác có tổng số đo hai góc đối nhau bằng 1800 thì tứ giác đó nội tiếp được đường tròn.
c) Các phương pháp chứng minh tứ giác nội tiếp.
 - Tứ giác có tổng hai góc đối nhau bằng 1800 .
- Tứ giác có 4 đỉnh cách đều một điểm (mà ta có thể xác định được). Điểm đó là tâm của đường tròn ngoại tiếp tứ giác.
- Tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh chứa hai đỉnh còn lại dưới một góc α.
2.2. Thực trạng của vấn đề trước khi áp dụng sáng kiến kinh nghiệm.
Từ thực tế giảng dạy bộ môn Toán học của bản thân tôi cũng như khi trao đổi, tham khảo nơi các đồng nghiệp khác thì gần như 100% học sinh học phân môn Hình học kém hơn Đại số. Cũng vì thế mà các em có tâm lí ngại học, không thích học, không có hứng thú học Hình học. Bởi vậy các em chưa thực sự nghiên cứu, tìm tòi, đào sâu suy nghĩ về một đơn vị kiến thức hình học nào đó, có chăng thì cả lớp vài chục em cũng chỉ được một vài em lưu tâm, để ý đọc thêm sách tham khảo, làm thêm các bài tập khó liên quan đến nội dung vừa học.
Thời điểm sau khi dạy xong chương III: Góc với đường tròn - Hình học 9: ở năm học 2016-2017, tôi tiến hành khảo sát mức độ tiếp thu kiến thức của các em học sinh lớp 9B thông qua một bài kiểm tra 45 phút với nội dung tập trung chủ yếu là phần kiến thức về tứ giác nội tiếp. Kết quả thu được như sau:
Tổng số HS
Giỏi
Khá
TB
Yếu
Kém
SL
%
SL
%
SL
%
SL
%
SL
%
23
01
4,3
05
21,7
10
43,5
04
17,4
03
13,1
Trong đó: Với ý khó dùng để phân loại đối tượng học sinh trong đề thi thì 01 em đạt loại giỏi ở mức 9 điểm mới chỉ đang làm dở; 05 em đạt loại khá ở mức 7 điểm thì chưa làm đến, còn lại số học sinh đạt điểm trung bình trở xuống có chất lượng bài làm rất hạn chế.
2.3. Các giải pháp đã sử dụng để giải quyết vấn đề.
2.3.1. Xây dựng hệ thống bài tập minh họa cách vận dụng trực tiếp kiến thức cơ bản về tứ giác nội tiếp.
Bài toán 1: Cho ABC. Hai đường cao BE và CF cắt nhau tại H. Gọi D là điểm đối xứng của H qua trung điểm M của BC. Chứng minh rằng tứ giác ABDC nội tiếp được trong một đường tròn. [2]
A
B
C
H
E
F
M
D
Bài giải: 
Vì tứ giác BHCD có hai đường chéo 
BC và HD cắt nhau tại trung điểm của mỗi 
đường nên là hình bình hành.
 CD // BH; DB // CH
 CD // BE; DB // CF
Mà BE AC; CFAB
 CD AC; DB AB
 ACD = ABD = 900 
Xét tứ giác ABDC có: ACD + ABD = 900 + 900 = 1800.
Suy ra tứ giác ABDC nội tiếp được trong một đường tròn (đpcm).
Nhận xét: Trong bài này, để chứng minh tứ giác ABDC nội tiếp, ta đã sử dụng phương pháp: Tứ giác có tổng hai góc đối nhau bằng 1800 .
Bài toán 2:
Cho đường tròn (O) đường kính AB và tia tiếp tuyến Bx của đường tròn. Trên tia Bx lấy hai điểm C và D (C nằm giữa B và D). Các tia AC và AD lần lượt cắt đường tròn tại E và F. Hai dây AE và BF cắt nhau tại M. Hai tia AF và BE cắt nhau tại N. Chứng minh rằng các tứ giác FNEM,CDFE nội tiếp.[2]
Bài giải: 
E
F
A
B
D
C
M
N
.O
x
*Vì AFB, AEB là các góc nội tiếp chắn nửa đường tròn (O)
 AFB = AEB = 900
 NFM = NEM = 900
Xét tứ giác FNEM có:
NFM + NEM = 900 + 900 = 1800
Suy ra tứ giác FNEM nội tiếp.
	*Ta có: FEA = FBA
 (hai góc nội tiếp cùng chắn FA ) (1)
FBA = FDB (cùng phụ FBD) (2)
Từ (1) và (2) FEA = FDB hay FEA = FDC
Mà FEA + FEC = 1800 (hai góc kề bù)
 FDC + FEC = 1800 
Tứ giác CDFE nội tiếp (đpcm).
Nhận xét: Trong bài này, để chứng minh cho tổng hai góc đối nhau của tứ giác CDFE bằng 1800 , ta đã đi chứng minh tứ giác này có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó.
Bài toán 3: Cho ABC không có góc tù. Các đường cao AH và đường trung tuyến AM không trùng nhau sao cho BAH = CAM. Gọi N là trung điểm của AB. Chứng minh AMHN là một tứ giác nội tiếp.[2]
Bài giải: 
A
N
M
H
B
C
Vì AHB vuông tại H có HN là 
đường trung tuyến ứng với cạnh huyền AB
NAH cân tại N
 NAH = AHN
Mà NAH = BAH = CAM (gt)
AHN = CAM (1)
Mặt khác MN là đường trung bình của ABC MN // AC 
 AMN = CAM (hai góc đồng vị) (2)
Từ (1) và (2) AHN = AMN
Xét tứ giác AMHN có hai đỉnh kề nhau H và M cùng nhìn cạnh AN dưới một góc bằng nhau AMHN là một tứ giác nội tiếp (đpcm).
Nhận xét: Trong bài này, để chứng minh tứ giác AMHN nội tiếp, ta đã sử dụng phương pháp: Tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh chứa hai đỉnh còn lại dưới một góc α.
A
B
C
H
I
K
M
.
O
Bài toán 4: Cho ABC nội tiếp đường tròn (O). Gọi M là điểm bất kì nằm trên đường tròn (O) (M khác A, B, C). Từ M kẻ MH AB; MIAC; MK BC (H AB; I AC; K BC). Chứng minh rằng 3 điểm H, I, K thẳng hàng.[5]
Bài giải: 
Xét tứ giác MIKC có 2 đỉnh I và K cùng 
nhìn cạnh MC dưới 1 góc vuông nên
là tứ giác nội tiếp
MIK + MCK = 1800
Hay: MIK + MCB = 1800 (1)
Vì AMCB là tứ giác nội tiếp nên:
MAB + MCB = 1800 
Mà MAB + HAM = 1800 (hai góc kề bù)
 MCB = HAM (2)
Xét tứ giác AIMH có 2 đỉnh I và H cùng nhìn cạnh AM dưới 1 góc vuông nên là tứ giác nội tiếp
 HAM = HIM (hai góc nội tiếp cùng chắn HM ) (3)
Từ (1), (2), (3) MIK + HIM = 1800 HIK = 1800
 HIK là góc bẹt 3 điểm H, I, K thẳng hàng (đpcm).
Nhận xét: Trong bài này:
 - Để chỉ ra các tứ giác MIKC, AIMH nội tiếp, ta đã sử dụng kiến thức về quỹ tích cung chứa góc: Qũy tích các điểm nhìn đoạn thẳng AB cho trước dưới một góc vuông là đường tròn đường kính AB.
- Để chứng tỏ được 3 điểm H, I, K thẳng hàng, ta đã phải sử dụng đến tính chất tổng hai góc đối nhau của tứ giác nội tiếp bằng 1800 trong hai tứ giác MIKC, AMCB.
- Đường thẳng HIK được gọi là đường thẳng Xim-xơn của điểm M (Robert Simson, 1687-1768, nhà toán học Xcôt-len).
2.3.2. Khai thác lời giải bài toán dựa vào tứ giác nội tiếp.
Trong phần này, ta sẽ đi khai thác kiến thức về tứ giác nội tiếp thông qua việc thêm hoặc bớt hoặc thay đổi một vài yếu tố của giả thiết bài toán, dẫn đến sự thay đổi kết luận của bài toán, từ đó tạo nên sự lôi cuốn, thích thú và niềm đam mê môn học đối với học sinh. 
Bài toán xuất phát 1:
Cho điểm M nằm ngoài đường tròn (O). Vẽ tiếp tuyến MA, MB với đường tròn (A, B là các tiếp điểm). Vẽ cát tuyến MCD không đi qua tâm O (C nằm giữa M và D). Tia MO cắt AB và (O) lần lượt tại H và K (H nằm giữa M và K). Chứng minh rằng:
Tứ giác MAOB nội tiếp
MC.MD = MA2
OH.OM + MC.MD = MO2
M
A
B
D
C
H
O
K
CK là tia phân giác DCH. (Đề thi vào 10 năm 2012-2013-Tỉnh Nghệ An)
Bài giải:	
Vì MA, MB là các tiếp tuyến của đường tròn (O) 
MA OA, MB OB
Xét tứ giác MAOB có: MAO + MBO = 900 + 900 = 1800
Suy ra tứ giác MAOB nội tiếp (đpcm).
b) Xét và có AMC chung, MAC = MDA (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn AC ) 
 (g . g)
(đpcm).
Xét vuông tại A, có AH MO 
 OH.OM = OA2
OH.OM + MC.MD = OA2 + MA2 (1)
Mặt khác áp dụng định lí Pi-ta-go vào vuông tại A ta có: (2)
Từ (1) và (2) OH.OM + MC.MD = MO2 (đpcm).
 Xét vuông tại A, có AH MO 
 MH.MO = MA2 , mà MC.MD = MA2 (theo câu b)
 MH.MO = MC.MD 
Xét và có: CMH chung, (cmt)
 (c.g.c) MCH = MOD
Mà MCH + HCD = 1800 (hai góc kề bù)
 MOD + HCD = 1800
 Tứ giác CDOH nội tiếp DCH = DOK (cùng bù HOD) (3)
Mặt khác: DCK =DOK (=sđ DK ) (4)
Từ (3) và (4) DCK = DCH CK là tia phân giác DCH (đpcm).
Nhận xét: Trong bài toán trên, nếu ta gọi I là giao điểm còn lại của MO và đường tròn (O), thì sẽ có ICK = 900 (góc nội tiếp chắn nửa đường tròn), tức là CI CK. Mặt khác MCH và HCD là hai góc kề bù, nên từ chỗ CK là tia phân giác DCH thì cũng sẽ suy ra được CI là tia phân giác của MCH. Do vậy ta có bài toán mới sau đây:
Bài toán 2:
M
A
D
C
H
O
I
K
Cho điểm M nằm ngoài đường tròn (O). Vẽ tiếp tuyến MA với đường tròn (A là tiếp điểm). Vẽ cát tuyến MCD nằm giữa hai tia MA và MO (C nằm giữa M và D). Kẻ AH vuông góc với MO tại H. Tia MO cắt (O) tại I (I nằm giữa M và H). Chứng minh rằng: CI là tia phân giác MCH. 
Bài giải:
Kéo dài MO cắt đường tròn (O) tại K.
Ta có: (g . g) MA2 = MC.MD 
 vuông tại A, có AH MO MA2 = MH.MO
 MC.MD = MH.MO 
 (c.g.c) MCH = MOD
Mà MCH + HCD = 1800 (hai góc kề bù)
 MOD + HCD = 1800
 Tứ giác CDOH nội tiếpDCH = DOK ( cùng bù HOD) (1)
Mặt khác: DCK =DOK (=sđ DK ) (2)
Từ (1) và (2) DCK = DCH CK là tia phân giác DCH. 
Mà ICK = 900 (góc nội tiếp chắn nửa đường tròn) 
 CI CK 
Mặt khác MCH và HCD là hai góc kề bù
 CI là tia phân giác MCH (đpcm).
Nhận xét: Trong bài toán trên, khi nối D với H thì dựa vào tứ giác CHOD nội tiếp ta cũng có thể suy ra được CHM = DHO, từ đó suy ra CHA = DHA. Do vậy ta lại có bài toán mới sau đây:
Bài toán 3:
M
A
D
C
H
O
Cho điểm M nằm ngoài đường tròn (O). Vẽ tiếp tuyến MA với đường tròn (A là tiếp điểm). Vẽ cát tuyến MCD nằm giữa hai tia MA và MO (C nằm giữa M và D). Kẻ AH vuông góc với MO tại H. Chứng minh rằng: HA là tia phân giác CHD.[3]
Bài giải:
Ta có: (g . g) MA2 = MC.MD 
 vuông tại A, có AH MO MA2 = MH.MO
 MC.MD = MH.MO 
 (c.g.c) MCH = MOD
Mà MCH + HCD = 1800 (hai góc kề bù)
 MOD + HCD = 1800 
 Tứ giác CDOH nội tiếp CDO + CHO = 1800 
Mà CHM + CHO = 1800 (hai góc kề bù)
 CHM = CDO (1)
Vì OC = OD OCD cân tại O CDO = OCD (2)
Lại có: OCD = OHD (hai góc nội tiếp cùng chắn OD của đường tròn ngoại tiếp tứ giác CDOH) (3)
Từ (1), (2), (3) CHM = OHD
Mặt khác: CHM + CHA = OHD + DHA = 900
CHA = DHA
 HA là tia phân giác CHD (đpcm).
Nhận xét: Trong bài toán trên, nếu gọi P là giao điểm của AH và CD thì ta có HP là tia phân giác góc trong tại đỉnh H của CHD, kết hợp với điều kiện HP HM ta có HM là tia phân giác góc ngoài tại đỉnh H của CHD. Khi đó theo tính chất đường phân giác trong tam giác ta sẽ có được gì? Lúc này nếu ta bổ sung thêm giả thiết của bài toán bằng việc qua điểm C kẻ đường thẳng song song với AD cắt AH, MA lần lượt tại I, K . Gọi N là điểm đối xứng với A qua D thì ta sẽ lại có bài toán mới nào?
Bài toán 4:
M
A
D
C
O
I
K
P
N
HI
 Cho điểm M nằm ngoài đường tròn (O). Vẽ tiếp tuyến MA với đường tròn (A là tiếp điểm). Vẽ cát tuyến MCD nằm giữa hai tia MA và MO (C nằm giữa M và D), Kẻ AH vuông góc với MO tại H, AH cắt CD tại P. Qua điểm C kẻ đường thẳng song song với AD cắt AH, MA lần lượt tại I, K . Gọi N là điểm đối xứng với A qua D. Chứng minh rằng: M, I, N thẳng hàng.[7]
Bài giải:	
Ta có: (g . g) MA2 = MC.MD 
 vuông tại A, có AH MO MA2 = MH.MO
 MC.MD = MH.MO 
 (c.g.c) MCH = MOD 
Mà MCH + HCD = 1800 (hai góc kề bù)
 MOD + HCD = 1800 
 Tứ giác CDOH nội tiếp CDO + CHO = 1800 
Mà CHM + CHO = 1800 (hai góc kề bù)
 CHM = CDO (1)
Vì OC = OD OCD cân tại O CDO = OCD (2)
Lại có: OCD = OHD (hai góc nội tiếp cùng chắn OD của đường tròn ngoại tiếp tứ giác CDOH) (3)
Từ (1), (2), (3) CHM = OHD
Mặt khác: CHM + CHA = OHD + DHA = 900
CHA = DHA
 HA là tia phân giác CHD 
Mặt khác: HA HM HM là tia phân giác góc ngoài tại đỉnh H của CHD. Theo tính chất đường phân giác trong tam giác, ta có:
; (4)
Vì CK // AD nên theo hệ quả của định lí Ta-lét, ta có: 
(5)
Vì CI // AD nên theo hệ quả của định lí Ta-lét, ta có: (6)
Từ (4), (5), (6) KC = CI KI = 2KC.
Vì N đối xứng với A qua D D là trung điểm đoạn thẳng AN 
 AN = 2AD.
Khi đó, từ (5), ta có: 
Xét MKI và MAN, có:
MKI = MAN (đồng vị)
 (cmt)
 MKI MAN (c.g.c) KMI = AMN, hay AMI = AMN
 Hai tia MI và MN trùng nhau 3 điểm M, I, N thẳng hàng (đpcm).
Nhận xét: 
- Trong chuỗi bài toán trên, ta thấy nút thắt nằm ở chỗ chỉ ra được tứ giác CDOH nội tiếp.
- Trong bài toán 1, nếu ta bỏ đi tiếp tuyến MB và thay đổi giả thiết thành: ‘‘Kẻ AH vuông góc với MO tại H. Gọi N là trung điểm dây CD, B là giao điểm của ON và AH’’ thì ta có bài toán sau đây: 
Bài toán 5:
Cho điểm M nằm ngoài đường tròn (O). Vẽ tiếp tuyến MA với đường tròn (A là tiếp điểm). Vẽ cát tuyến MCD nằm giữa hai tia MA và MO (C nằm giữa M và D). Kẻ AH vuông góc với MO tại H. Gọi N là trung điểm dây CD, B là giao điểm của ON và AH Chứng minh rằng:
Các tứ giác MANO và BHOD nội tiếp.
M
A
D
C
H
O
N
B
K
b) Khi 3 điểm M, C, D cố định trên cát tuyến của đường tròn (O) thì tâm đường tròn ngoại tiếp tam giác ONH luôn chạy trên một đường thẳng cố định khi đường tròn (O) thay đổi.[6]
Bài giải:
* Vì MA là tiếp tuyến của đường tròn (O) MA OA
Vì N là trung điểm CDON CD
Xét tứ giác MANO có hai đỉnh kề nhau A và N cùng nhìn cạnh MO dưới một góc vuông Tứ giác MANO nội tiếp (đpcm). 
* Xét OHB và ONM có: HON chung, OHB = ONM (= 900) 
OHB ONM (g . g)
 ON.OB = OH.OM (1)
Xét vuông tại A, có AH MO 
 OH.OM = OA2 = OD2 (2)
Từ (1) và (2) ON.OB = OD2 
Xét ODB và OND có: DON chung, (cmt)
ODB OND (c.g.c)
 ODB = OND = 900
Xét tứ giác BHOD có: BHO + BDO = 900 + 900 = 1800
Suy ra tứ giác BHOD nội tiếp (đpcm).
Gọi K là giao điểm của CD và AH.
* Xét MHK và MNO có: HMK chung, MHK = MNO (= 900) 
MHK MNO (g . g)
 MH.MO = MN.MK (3)
Xét vuông tại A, có AH MO 
 MH.MO = MA2
Lại có: (g . g) 
 MA2 = MC.MD 
 MH.MO = MC.MD (4)
Từ (3) và (4) MN.MK = MC.MD 
Vì M, C, D cố định trung điểm N của CD cố định không đổi điểm K cố định.
Xét tứ giác KHON có: KHO + KNO = 900 + 900 = 1800
Suy ra tứ giác KHON nội tiếp
Vì đường tròn ngoại tiếp tứ giác KHON cũng chính là đường tròn ngoại tiếp tam giác ONH, mà đường tròn này luôn đi qua hai điểm cố định K và N do đó tâm đường tròn này nằm trên đường trung trực của đoạn thẳng KN
Vậy khi 3 điểm M, C, D cố định trên cát tuyến của đường tròn (O) thì tâm đường tròn ngoại tiếp tam giác ONH luôn chạy trên một đường thẳng cố định (là đường trung trực của đoạn thẳng KN) khi đường tròn (O) thay đổi (đpcm).
Nhận xét: 
- Trong bài toán trên, để giải quyết được ý b, ta đã sử dụng nhận xét: đường tròn ngoại tiếp tứ giác KHON cũng chính là đường tròn ngoại tiếp tam giác ONH. Vậy nên việc chỉ ra tứ giác KHON nội tiếp tuy đơn giản xong đó lại là nút thắt để giải quyết bài toán. 
-Trong bài toán 1, nếu ta thay đổi giả thiết: “Tia MO cắt AB và (O) lần lượt tại H và K (H nằm giữa M và K)’’ thành: Gọi I là trung điểm CD, Tia BI cắt đường tròn (O) tại K, thì ta có bài toán sau đây: 
Bài toán 6:
M
A
B
D
C
O
K
I
x
Cho điểm M nằm ngoài đường tròn (O). Vẽ tiếp tuyến MA, MB với đường tròn (A, B là các tiếp điểm). Vẽ cát tuyến MCD nằm giữa hai tia MA và MO (C nằm giữa M và D). Gọi I là trung điểm CD, Tia BI cắt đường tròn (O) tại K . Chứng minh rằng: AK // CD.[4]
Bài giải:	
Vì MA, MB là các tiếp tuyến của đường tròn (O) 
MA OA, MB OB
Vì I là trung điểm CDOI CD
Vì 3 điểm A, I, B cùng nhìn đoạn thẳng MO dưới một góc vuông nên chúng cùng thuộc đường tròn đường kính MO, tức là 5 điểm M, A, I, O, B cùng thuộc đường tròn đường kính MO
 AMI = ABI (hai góc nội tiếp cùng chắn AI ) 
Mà xAK = ABK = ABI (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn AK )
 xAK = AMI, mà hai góc này lại nằm ở vị trí đồng vị
AK // MI AK // CD (đpcm).
Nhận xét: Trong bài toán 1, nếu ta thay đổi giả thiết: “Tia MO cắt AB và (O) lần lượt tại H và K (H nằm giữa M và K)’’ thành: ‘‘Đường thẳng đi qua C và vuông góc với OA cắt AB, AD theo thứ tự ở H và K’’, thì ta có bài toán sau đây: 
Bài toán 7:
Cho điểm M nằm ngoài đường tròn (O). Vẽ tiếp tuyến MA, MB với đường tròn (A, B là các tiếp điểm). Vẽ cát tuyến MCD không đi qua tâm O (C nằm giữa M và D). Đường thẳng đi qua C và vuông góc với OA cắt AB, AD theo thứ tự ở H và K. Chứng minh rằng: CH = HK.[3]
M
A
B
D
C
O
H
K
I
Bài giải:	
Kẻ OI CD (I CD) IC = ID.
Vì MA, MB là các tiếp tuyến của đường tròn (O) 
MA OA, MB OB
Vì 3 điểm A, I, B cùng nhìn đoạn thẳng MO dưới một góc vuông nên chúng cùng thuộc đường tròn đường kính MO, tức là 5 điểm M, A, I, O, B cùng thuộc đường tròn đường kính MO
 AMI = ABI (hai góc nội tiếp cùng chắn AI ) (1)
Ta lại có: MA // CK (cùng OA)
 AMI = HCI (hai góc đồng vị) (2)
Từ (1) và (2) ABI = HCI HBI = HCI 
Xét tứ giác CHIB có hai đỉnh kề nhau C và B cùng nhìn cạnh HI dưới một góc bằng nhau CHIB là tứ giác nội tiếp HIC = HBC (hai góc nội tiếp cùng chắn HC) 
Mặt khác: HBC = ABC = ADC (hai góc nội tiếp cùng chắn AC )
HIC = ADC, mà hai góc này lại ở vị trí đồng vị
 HI // AD HI // KD
Xét CKD có: IC = ID; HI // KD (cmt)
HC = HK (đpcm).
Nhận xét: 
- Nút thắt của bài toán này nằm ở việc chỉ ra tứ giác CHIB nội tiếp.
-Trong bài toán 1, nếu ta thay đổi giả thiết: “Tia MO cắt AB và (O) lần lượt tại H và K (H nằm giữa M và K)’’ thành: ‘‘Kẻ đường kính BON. Các đường thẳng NC, ND cắt đường thẳng MO lần lượt tại E và F’’. thì ta có bài toán sau đây: 
Bài toán 8:
Cho điểm M nằm ngoài đường tròn (O). Vẽ tiếp tuyến MA, MB với đường tròn (A, B là các tiếp điểm). Vẽ cát tuyến MCD không đi qua tâm O (C nằm giữa M và D). Kẻ đường kính BON. Các đường thẳng NC, ND cắt đường thẳng MO lần lượt tại E và F. Chứng minh rằng: OE = OF.[3]
M
A
B
D
C
O
N
E
F
H
Bài giải:	
Vì MA, MB là các tiếp tuyến của đường tròn (O) 
MA OA, MB OB
Xét tứ giác MAOB có: MAO + MBO = 900 + 900 = 1800
Tứ giác MAOB nội tiếp 
AMO = ABO (hai góc nội tiếp cùng chắn AO )
Mà ABO = ABN = CAN (hai